Page 329 - Learning to Learn

LEARNING TO LEARN: BECOMING A SELF -GROWER 329
EXPERIENCE 11: METACOGNITION : THINKING ABOUT MY THINKING READING
GENERALIZING Helping Learners Make the
Shift from Doing to THINKING
In many disciplines, learners are required to do a lot of homework in order to produce the ability to apply the
concepts, processes, and principles of the discipline to a variety of contexts. Even with all these homework
problems, many students still complain when they encounter a problem in a new or unfamiliar context on the
test. What does this mean? That they haven’t truly generalized the knowledge. What are the ramifications of
this? Faculty members teaching the next or follow-on course recognize that students are unable to transfer
knowledge from the previous course to the current course.
As a way to help students build the skills necessary for generalizing and transferring knowledge, one of
the best practices is called Generalization after Four Problems. The approach is to have students become
increasingly able to generalize concepts, processes, and principles by:
1. Solving a problem in a familiar context
2. Solving a problem in a similar context
3. Solving a problem in a more difficult (less similar, less familiar) context
4. Solving a problem in a very difficult (least similar, least familiar) context
This is a very useful practice and will help students increase their ability to generalize.
But there is a technique that may be evenmore promising: Having students create their own “hard problem.”
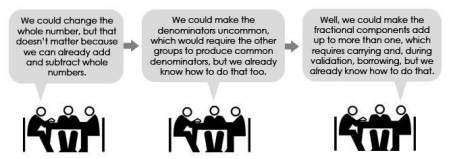
In a recent basic math course an instructor was asked to observe, groups of students were working on adding
and subtracting mixed numbers. One group had just finished a problem and said that they found it was a “really
hard” problem. The instructor intervened with a challenge, asking them to create another “hard problem” that
would stump the other student groups. The thinking they exhibited was interesting:
How many more problems do they need to do after they’ve
gone through that thinking and realized the extent of variation
of the problem across any other context? None! They have
grasped the variables that allow for variability — the very
definition of what it means to generalize.
If instructors are willing to identify what it is that varies across
contexts, they are able to produce the critical thinking questions
that encourage high-quality learning. Having learners do the
same produces and improves the ability to generalize.