Our curricula offerings in Mathematics has a new member in the Foundations of Mathematics Activity Book. While the content focus is the same as Foundations of Mathematics, the activities themselves are, first and foremost, interactive. We have taken all of our expertise in how students learn best and most effectively — through engaged discovery and active problem-solving — and used that as the basis for this book. This is not a textbook; there are no long discursive passages about place values or the various properties of addition. There are a thousand textbooks that offer that kind of informational content. What we offer is a kind of practical math laboratory where students take the information their textbook imparts and work with it, play with it, and explore it. It is precisely through this kind of active and interactive exploration that students begin to take ownership of their learning.

But because a picture is worth a thousand words (and as surprising as it may be, we are aware of our tendency toward verbosity on topics that excite us), we'd like to share a few samples of the exciting and powerful features of these activities, as well as some of the thinking behind those features. 

Each activity begins with a real-world math problem. Students should be able to solve this problem, if they have both knowledge and comprehension of the applicable information available in their math textbook. This is an instance of application, the third level of Bloom's Taxonomy. 

Once students have completed the contextualized math problem, they are given the opportunity to self-assess their readiness to do more. The dimensions of this assessment are taken from the core learning objectives for the math content (i.e.,  what students should understand, if they have truly learned).

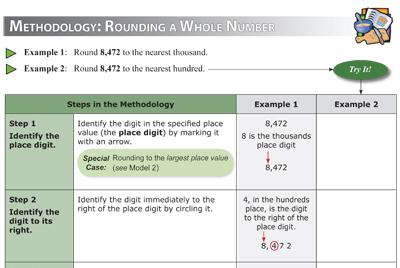In learning processes, students often resort to memorizing what an instructor models. Since the steps are not generalized, students see each context as new knowledge to memorize and find it impossible to generalize from a set of examples and practice problems. By providing a concrete model of the process, learners can analyze how each step supports the process, helping them quickly and effectively arrive at a verifiable solution. The most important Innovation is Example 2, an opportunity for students to complete a "Try It!" problem, side-by-side with the given example. The goal of this is to help students immediately generalize their understanding beyond a single example. Students must begin to see  that even if the specifics of the information changes, the rules, steps, and processes remain the same. 

Models are contextually worked-out examples that demonstrate the steps of the methodology in solving given problems.

An activity always uses multiple models that illustrate new contexts even as they advance in difficulty so learners can compare and contrast the models to further generalize the methodology. Complete modeling is presented, including validation.

Models are a critical step in the Learning Process Methodology, and are one of the most time-tested pedagogical techniques because the illustration of the expert makes the context comes alive in meaning and understanding for the novice.

While we use models in all of our math curricula, the real innovation here is the "Make Your Own Model" component. Students are instructed to create a model demonstrating how to solve the most difficult problem they can think of.

Because students determine the problem, it is kept at a level of complexity they can handle (they are not likely to know enough yet to create a problem that the methodology does not address), while simultaneously maximizing their learning development through  increased challenge. Students enjoy challenging an instructor; they like to ask the "Yeah, but what about..." questions. This section harnesses that impulse and allows students to take increased ownership of their learning.

The Critical Thinking Questions are designed to maximize comprehension, meaning, and understanding. The range of learning issues associated with activity content is addressed with the complete set of questions. This component of the activity prepares the learner to be able to quickly transfer the knowledge to new context and after a few diverse exercises, allow the learner to generalize this knowledge to transfer across any appropriate context. 

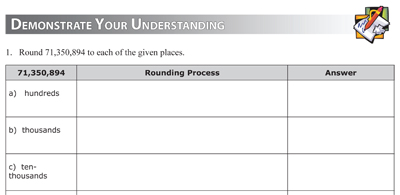This section continues to work on Level-3 knowledge (application). The problems provide students with a minimal set of challenging exercises to practice transferring and generalizing their knowledge so they can meet the performance criteria for the learning activity. The set of exercises provides a graduated level of difficulty to verify to the learner that they can address the various aspects of the use of the knowledge.

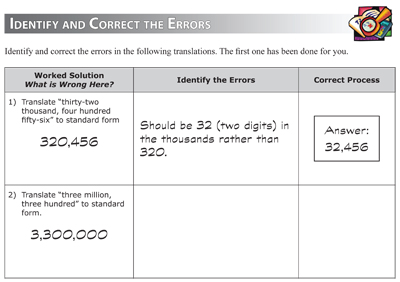Students are now given the opportunity to demonstrate their mastery of content by identifying and correcting errors made by others. Instructors understand how powerful this process is and how well it serves to increase understanding of the thinking and processes used in solving math problems.

When an answer does not validate, many students' first instinct is to erase the entire problem and begin again. This does not strengthen students' skills; in fact it is a behavior that has much in common with evaluation rather than assessment, as a judgment has been made (the answer is wrong) with no further analysis of where things went wrong. If students are led to discover the nature of the error, and then to demonstrate the correct process, assessment behavior is enforced, helping students to become stronger self-assessors, and more able to strengthen their own performance.